RNN-T 论文阅读
公式推导
定义:
- 定义任务输入:\(x = (x_1, x_2, \dots, x_T)\),其中 \(x\) 中的元素 \(x_i \in \mathcal{X}\),\(x \in \mathcal{X}^*\)。每一个\(x_i\) 一般为MFCC的倒谱系数构成的向量。
- 定义任务输出:\(y = (y_1, y_2, \dots, y_U)\),其中 \(y\) 中的元素 \(y_i \in \mathcal{Y}\),\(y \in \mathcal{Y}^*\)。每一个 \(y_i\) 一般是一个one-hot的向量,编码特定的phoneme。
- 定义集合 \(\bar{\mathcal{Y}} = \mathcal{Y} \cup \{\varnothing\}\),作用是在输出中加入一些\(\varnothing\)
- 定义函数 \(B: \bar{\mathcal{Y}}^* \to \mathcal{Y}^*\),作用是去除所有的 \(\varnothing\)
- 定义模型RNN-Transducer,输入是\(x\),输出是\(y\in \mathcal{Y}^*\),该模型的概率建模为:\(\Pr(y \in \mathcal{Y}^* | x)\)
由以上定义我们可以得知: \[\Pr(y \in \mathcal{Y}^* | x)=\sum_{a \in B^{-1}(y)} \Pr(a | x)\] 即我们需要枚举所有可能的添加 \(\varnothing\)的方式,把它们的概率相加,得到最终的概率。
下面开始,我们来想办法解决\(\sum\)内的部分,即 \(\Pr(a \in \bar {\mathcal{Y}}^* | x)\)
我们使用两个网络:
- Transcription Network:输入为 \(x\), 输出Transcription Vectors \(f=(f_1,f_2,...,f_T)\)(为了方便起见定义长度为\(T\),但实际上如果做pooling的话可能不是\(T\)
- Prediction Network:输入为 \(y\),输出为prediction vector \(g=(g_0,g_1,...,g_U)\)
Prediction Network
Prediction Network \(G\) 是一个RNN或LSTM。
目标:在给定过去的输出序列\(y\)时,预测下一个可能的输出元素。因此,它类似于标准的next-step prediction RNN(或LSTM),但额外允许预测\(\varnothing\)。
输入:\((\varnothing, y_1,y_2,...,y_U)\),即在\(y\)前面加了一个\(\varnothing\)。每个\(y_i\)采用one-hot编码,假设维度为K。
输出:\(g=(g_0,g_1,...,g_U)\),每个\(g_i\)维度为K+1(加上了\(\varnothing\))。
Transcription Network
- Transcription Network \(F\) 是一个双向RNN(或LSTM)。
- 输入为\(x\),也就是MFCC的系数向量序列。
- 输出为\(f\),同样为K+1维向量的序列(加上了\(\varnothing\))。
Output Distribution
我们回顾两个网络的输入输出:
- Transcription Network:输入 \(x\), 输出\(f=(f_1,f_2,...,f_T)\)
- Prediction Network:输入 \(y\),输出 \(g=(g_0,g_1,...,g_U)\)
接下来我们整合两个网络。定义: \[h(k,t,u)=e^{f_t^k+g_u^k}\]
其中\(1\leq t \leq T\), \(0 \leq u \leq U\),标签 \(k\in \bar{\mathcal{Y}}\)。\(k\)作为上标时表示向量的第\(k\)个元素。
归一化: \[\Pr(k \in \bar {\mathcal{Y}} | t,u)=\frac{h(k,t,u)}{\sum_{k'\in \mathcal{Y}}h(k',t,u)}\]
这个式子代表着:在\(f\)输出到\(t\),\(g\)输出到\(u\)时,预测为\(k\)的概率。而\(f_t^k\)和\(g_u^k\)可以直接相加的底气在于,他们都代表着同一意义的概率。
Q:为什么要枚举\(t\)和\(u\)呢?他们不应该都等于\(k\)吗?
A:因为存在\(\varnothing\),所以在同一个位置上,\(f\)和\(g\)并不一定进行到了同一个字符,所以需要枚举所有\(t\)和\(u\)。
实际上,由于\(g\)的输入是\(y\),它除了第一个字符是\(\varnothing\),后面的都是字符,而\(f\)却可能出现很多\(\varnothing\),因此他们大概率是对不齐的。
现在我们对比我们的目标式子:
\[\Pr(a \in \bar {\mathcal{Y}}^* | x)\]
我们还剩最后一步:对\(t\)和\(u\)进行累计,求出联合概率分布。
为了方便推导,我们定义两个记号:
\[ y(t,u) \equiv \Pr(y_{u+1} | t, u) \] \[ \varnothing(t, u) \equiv \Pr(\varnothing | t, u) \] 他们表示在\((t,u)\)这个节点上,预测出的为答案为字符或者\(\varnothing\)的概率。
Forward-Backward 算法
这个算法告诉我们
Forward算法
定义前向变量 \(\alpha(t, u)\) 为在 \(f[1:t]\) 中输出 \(y[1:u]\)的概率。所有 \(1 \leq t \leq T\) 和 \(0 \leq u \leq U\) 的前向变量可以通过递归计算:
\[ \alpha(t, u) = \alpha(t - 1, u) \varnothing(t - 1, u) + \alpha(t, u - 1) y(t, u - 1) \]
初始条件为:\(\alpha(1, 0) = 1\)
这个式子的意思是:在\(f[1:t]\)中输出 \(y[1:u]\)的概率,等于在\(f[1:t-1]\)中输出 \(y[1:u]\)的概率乘上在\((t,u)\)这个位置生成 \(\varnothing\) 的概率,加上在\(f[1:t]\)中输出 \(y[1:u-1]\)的概率乘上在\((t,u)\)这个位置生成字符的概率。
可以形象的表示为下图:
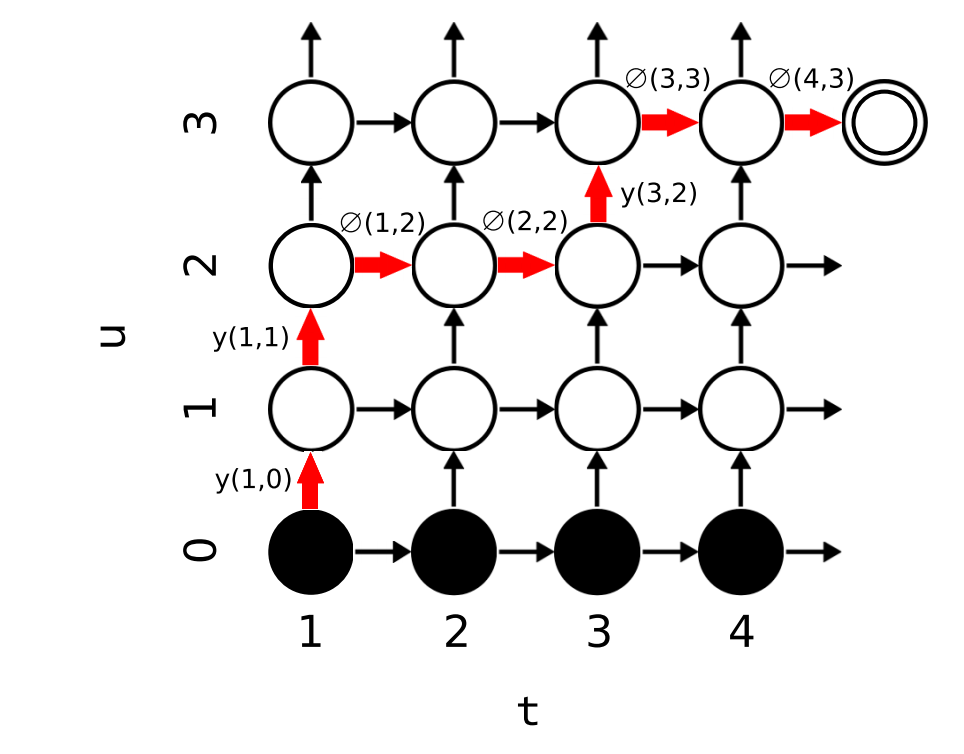
其中,底部的黑色节点表示在没有输出任何内容之前的空状态。
Backward算法
类似的,我们可以定义后向变量 \(\beta(t, u)\) 为在 \(f[t:T]\) 中输出 \(y[u+1:U]\) 的概率。
\[ \beta(t, u) = \beta(t + 1, u) \varnothing(t, u) + \beta(t, u + 1) y(t, u) \]
初始条件为:\(\beta (T,U) = \varnothing (T,U)\)
Loss 函数
至此,我们终于可以求出
\[\Pr(a \in \bar {\mathcal{Y}}^* | x) = \sum_{(t, u): t + u = n} \alpha(t, u) \beta(t, u) \]
也就是左上到右下对角线上\(\alpha(t, u) \beta(t, u)\) 的总和。
于是Loss函数就是: \[ L = - \ln Pr(y^* | x) \]