Pruned RNN-T 论文阅读
RNN-T 的缺点
- 损失函数计算相对较慢
- 占用较多内存
RNN-T模型需要储存一个4维的张量,维度是 \((N, T, U, C)\), 其中\(N\)是batch_size,\(T\)是Transcription Network的输出长度,\(U\)是Prediction的输出长度,\(V\)是词表大小。
本文将\(U\)限制为 \(S\subseteq U\),从而加速训练。
基本思想
仅计算对最终损失有重要贡献的 \((t,u)\) 对应项的joiner network,从而减少计算量。
具体来说,我们执行两次递推:
- 使用一个trivial的joiner network,该网络计算速度非常快。利用初步计算结果:确定哪些索引对损失贡献较大。
- 第二次计算:仅对筛选出的 \((t,u)\)子集来计算的joiner network。
Trivial Joiner Network
Trivial Joiner Network的思路为:
直接对encoder embedding和decoder embedding进行投影,得到未归一化的对数概率:
\[ L_{\text{enc}}(t, v) \]
\[ L_{\text{dec}}(u, v) \]
那么最终的loss就是:
\[L_{\text{trivial}}(t, u, v) = L_{\text{enc}}(t, v) + L_{\text{dec}}(u, v) - L_{\text{normalizer}}(t, u)\]
其中
\[ L_{\text{normalizer}}(t, u) = \log \sum_{v} \exp \left( L_{\text{enc}}(t, v) + L_{\text{dec}}(u, v) \right) \]
这个公式本质上是log-space的矩阵乘法,容易实现。
Pruning Bounds
引入常数\(S\),表示对于任意的\(t\),我们将仅计算考虑 \(L(t, u, v)\) 在\(p_t \leq u < p_t + S\) 位置上的值。其中 \(p_t\) 是通过Trivial Joiner Network得到的。
剪枝就是将 \(u < p_t\) 或 \(u \geq p_t + S\) 的 \(P(t, u, \cdot)\) 视为 \(-\infty\)。
理想情况下,我们希望找到一组整数剪枝边界 \(p = p_0, p_t, \dots, p_{T-1}\),该组边界能够最大化Trivial Joiner Network的总保留概率。换句话说,我们要最大化数据的似然性。
为了简化问题,我们通过为每个帧 \(t\) 找到局部最优的剪枝边界来解决,然后应用一些连续性约束来改进结果。
具体来说,就是求解下面这个公式:
\[p_t = \arg\max_{p=0}^{U-S+1} \left( - y'_0(t, p-1) + \sum_{u=p}^{p+S-1} \varnothing'_0(t, u) \right)\]
其中 \(y'_0(t, u)\) 和 \(\varnothing'_0(t, u)\) 是 \(L_{tot}\) 关于\(y(t, u)\) 和\(\varnothing(t, u)\).的导数。
这个公式可以形象的理解为下图中绿线减去红线的值。
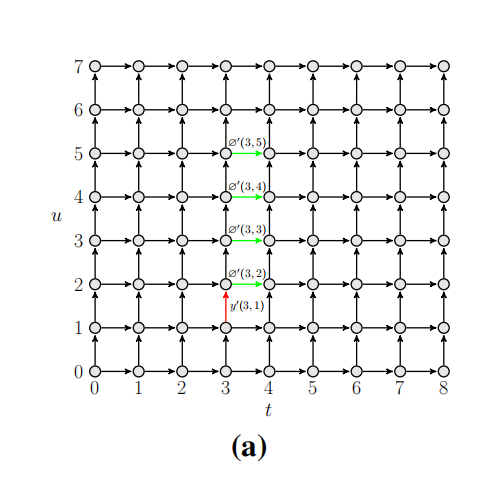
减去红线的原因是?
当然还需要满足一些条件(连续性等):
\[ 0 \leq p_t \leq U - S + 1 \]
\[ p_t \leq p_{t+1} \]
\[ p_{t+1} - p_t \leq S \]
Loss function
\[ L_{\text{smoothed}}(t, u, v) \]
\[ = (1 - \alpha_{\text{lm}} - \alpha_{\text{acoustic}}) \cdot L_{\text{trivial}}(t, u, v) + \alpha_{\text{lm}} \cdot L_{\text{lm}}(t, u, v) + \alpha_{\text{acoustic}} \cdot L_{\text{acoustic}}(t, u, v) \]
其中:
\[ L_{\text{trivial}}(t, u, v) = \text{LogSoftmax}_v \left( L_{\text{enc}}(t, v) + L_{\text{dec}}(u, v) \right) \]
\[ L_{\text{acoustic}}(t, u, v) = \text{LogSoftmax}_v \left( L_{\text{enc}}(t, v) + L_{\text{avg-dec}}(u, v) \right) \]
\[ L_{\text{lm}}(t, u, v) = \text{LogSoftmax}_v (L_{\text{dec}}(u, v)) \]
\[ L_{\text{avg-dec}}(u, v) = \log \left( \frac{1}{U + 1} \right) \sum_{u=0}^{X} \text{Softmax}_v L_{\text{dec}}(u, v) \]
为什么要平均?