HuBert论文阅读
概述
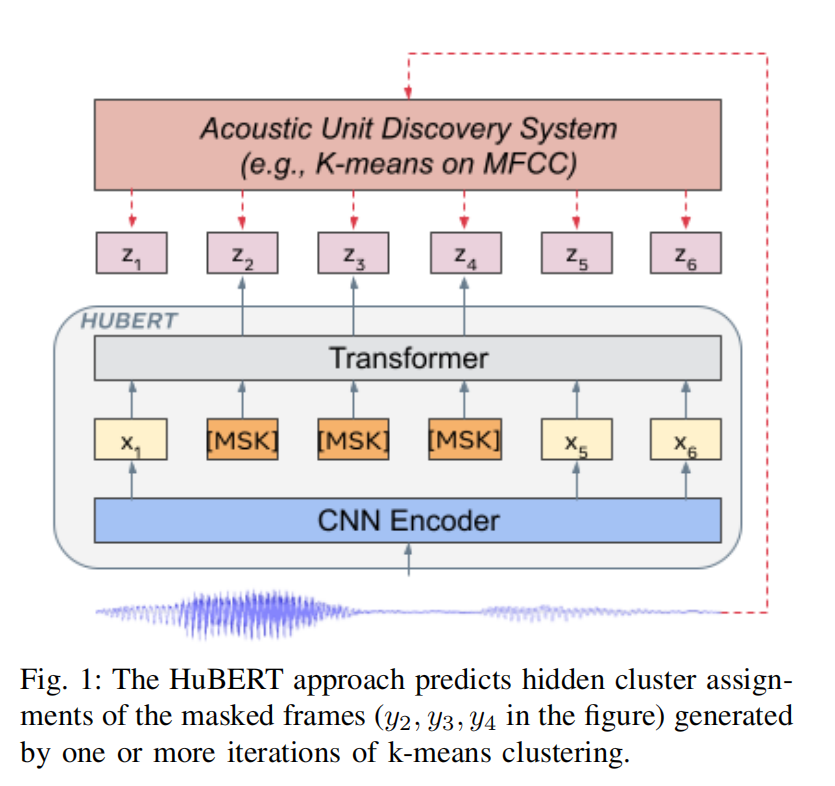
- 作用:从无监督数据中学习隐层表示。
- 端口:输入为音频,输出为隐层表示。
训练过程:
- 利用Acoustic Unit Discovery System得到label
- 通过HuBERT从mask之后的输入中得到隐层表示z
- 计算label和预测之间的loss
细节
Acoustic Unit Discovery
可以理解为语音离散化。
一些记号:
T个frame的语音 $ X = [x_1,..,x_T] $。Acoustic Unit Discovery模型输出的hidden units为 $ h(X)=Z=[z_1,..,z_T]$,其中 \(z_t \in [C]\) 是一个C-class的变量。h是一个非监督的聚类模型,如k-means on MFCC。
Mask
使用了和wav2vec 2类似的方法,首先选择 \(p%\) time-steps作为开始序号,然后从各个序号后面数 \(l\) 个steps作为要mask的区域。
假设\(M \subset [T]\) 为要mask的区域, \(\tilde{X}\) 表示被mask之后的输入,定义在mask区域上的entropy-loss为:
\[ L_m(f;X,M,Z)= \sum_{t\in M}logp_f(z_t|\tilde{X},t) \]
相应的定义不在mask区域上的enrtopy-loss:
\[ L_u(f;X,M,Z)= \sum_{t\notin M}logp_f(z_t|\tilde{X},t) \]
最终的loss为:
\[ L = \alpha L_m + (1-\alpha)L_u \]
loss公式中,\(p_f\)的公式如下;
\[ p_f^{(k)}(c | \tilde{X}, t) = \frac{\exp(\text{sim}(A^{(k)} o_t, e_c)/\tau )}{\sum\limits_{c' =1}^{C} \exp(\text{sim}(A^{(k)} o_t, e_{c'})/\tau )} \]
其中 \(A^{(k)}\) 是第k个聚类的投影矩阵,乘以 \(o_t\) 之后变成C-class的离散变量,其中 \([o_1, ..., o_T]\) 为Bert的输出。 \(e_c\) 是 \(c\) 的嵌入向量,\(sim(·,·)\) 是两个向量之间的余弦相似度。\(\tau\) 是logit scaling factor。
注意这几个变量分别代表什么。我们可以从两条路径来分析
音频通过Acoustic Unit Discovery模型,得到codewords \([z_1,..,z_T]\),这是一组离散的类别。每一个类别 \(c\) 我们赋予一个嵌入向量,这就是 \(e_c\),这是标签生成的路径。
音频通过HuBert之后得到 \([o_1, ..., o_T]\),乘以投影矩阵 \(A\),计算和标签的相似度。
Cluster Ensembles
k-means根据初始值和k值的不同,其表现也会大不相同。因此作者采用多个不同参数的k-means进行学习,这就是Cluster Ensembles。设用 \(Z^{(k)}\)表示第k个聚类模型生成的sequence。故此时:
\[ L_m(f;X,\{Z^{(k)}\}_k,M)=\sum_{t\in M} \sum_{k} log p_f^{k}(z_t^{k}|\tilde{X},t) \]
Iterative Refinement of Cluster Assignments
虽然可以直接在MFCCs这样的acoustic features上直接得到label,但随着学习的进行,这种label显得太过粗糙。因此,在学习进行到一定程度时,我们在模型学习到的表示上重新学习聚类模型来替代之前的聚类模型,提高了模型的精度。